Julia Set by CUDA
Published:
 Please refer to haoran0115/julia-set-cuda.
Please refer to haoran0115/julia-set-cuda.
Published:
 Please refer to haoran0115/julia-set-cuda.
Please refer to haoran0115/julia-set-cuda.
Published:
Problem. Show that in an hamiltonian system it is impossible to have asymptotically stable equilibrium positions and asymptotically stable limit cycles in the phase space.1
Arnol’d, V. I. (2013). Mathematical methods of classical mechanics (Vol. 60). Springer Science & Business Media. ↩
Published:
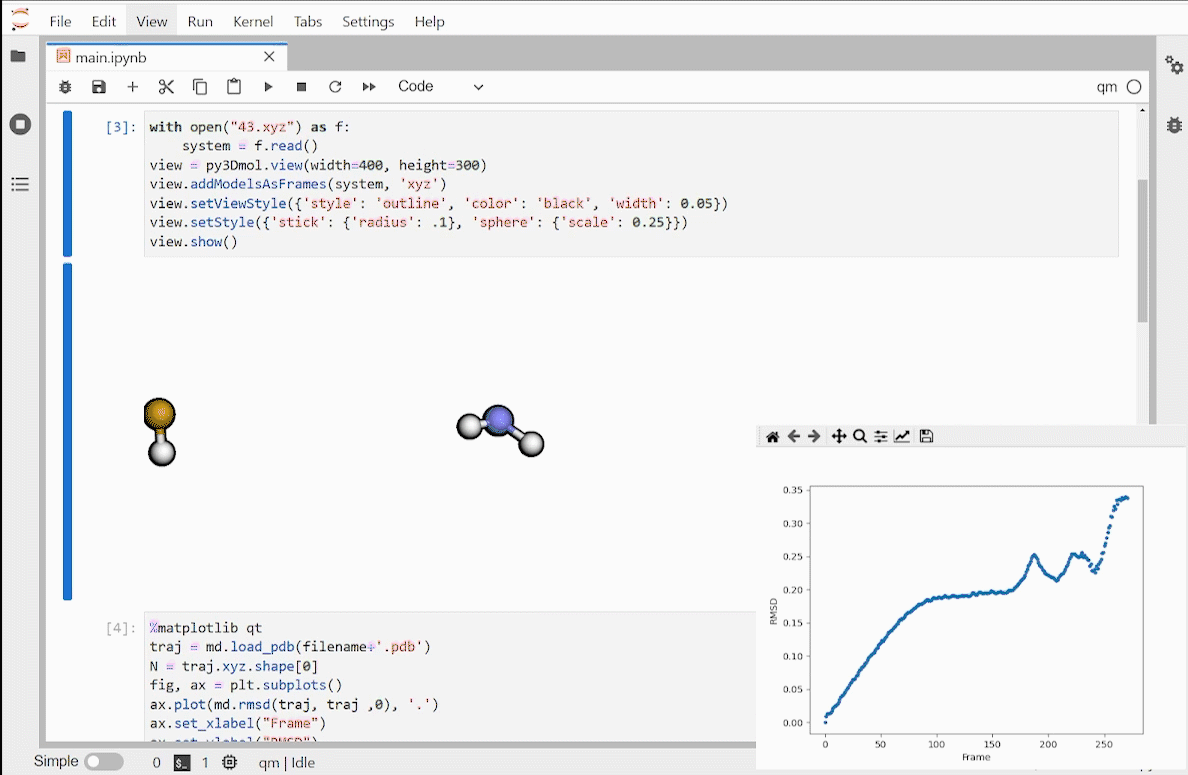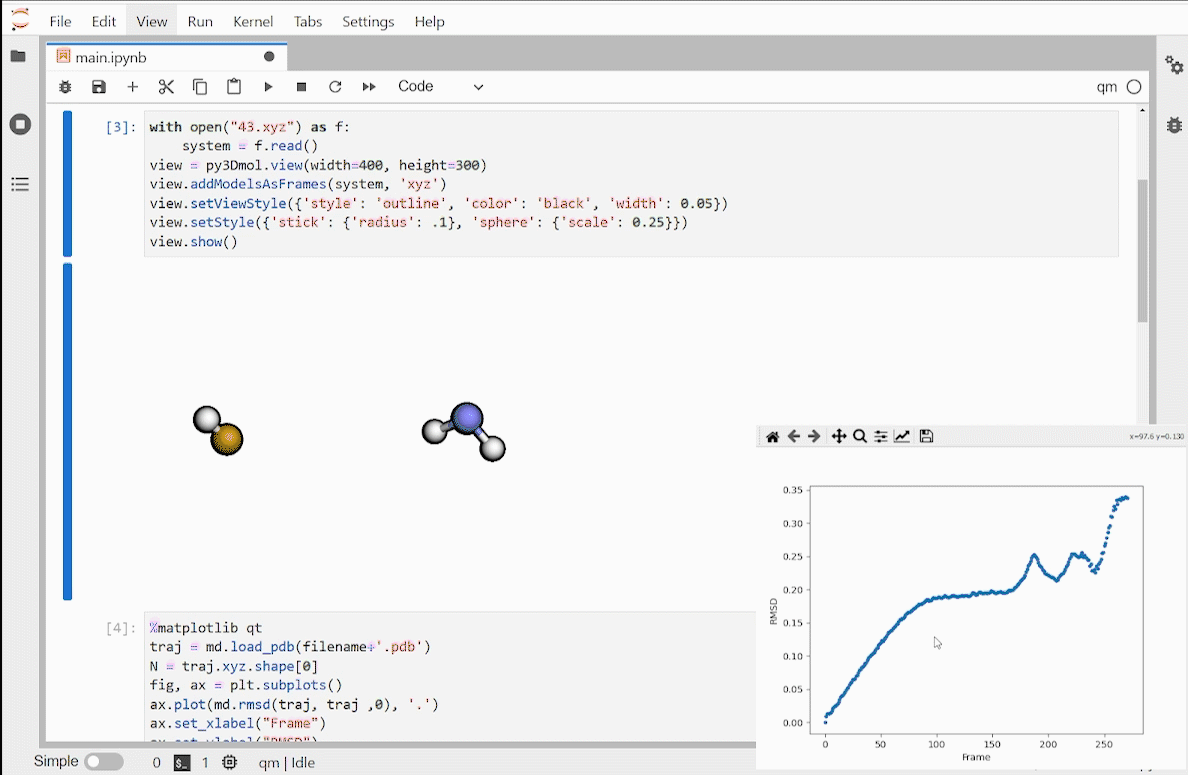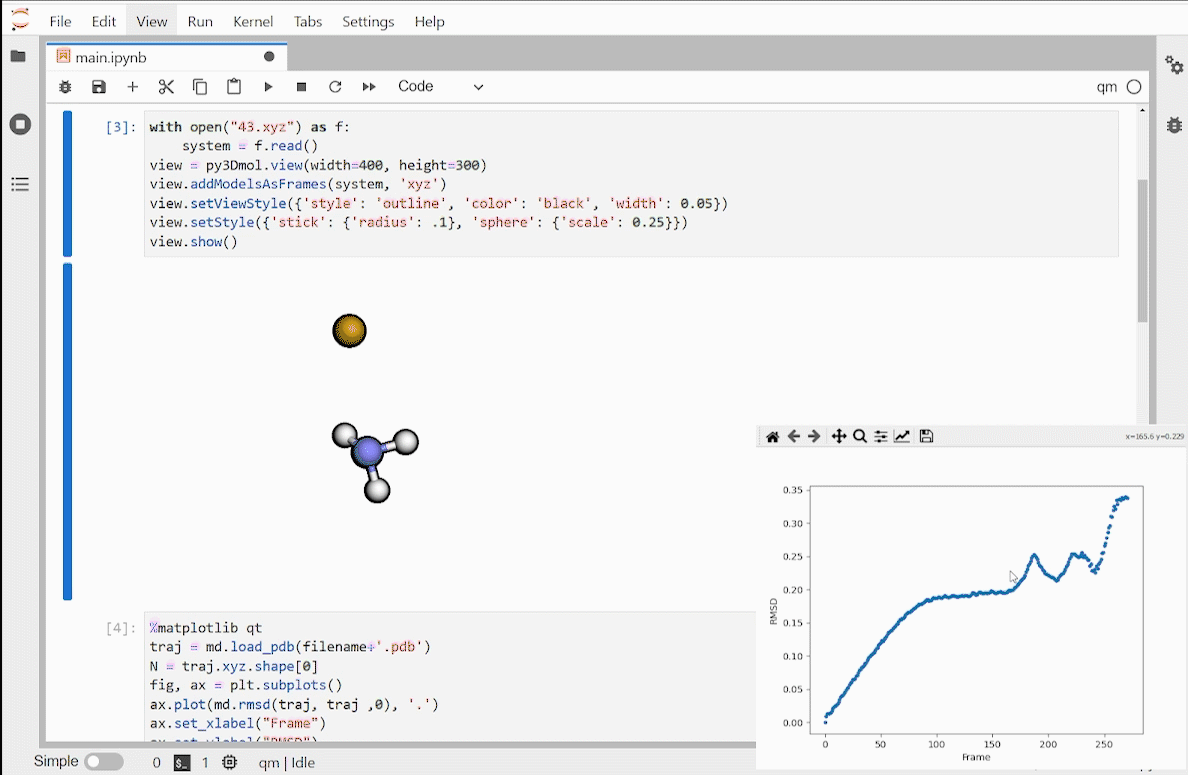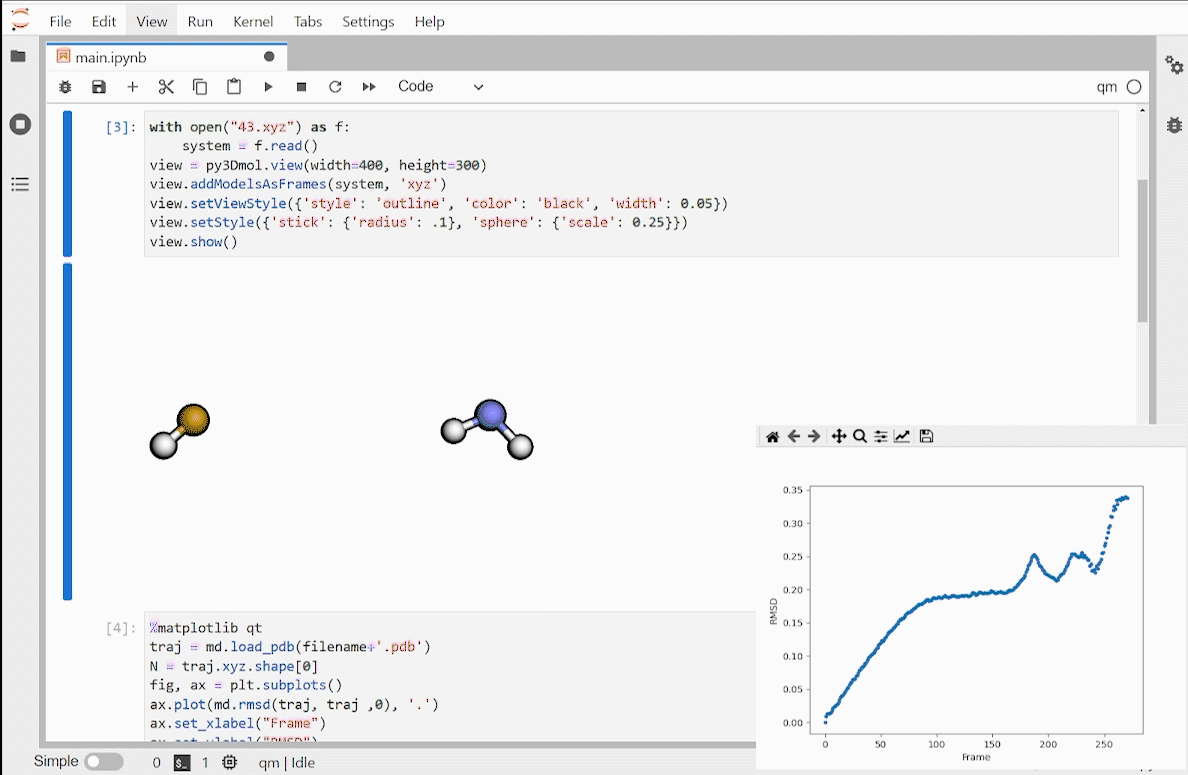
Published:
Problem. Prove Liouville's formula \(W=W_0 e^{\int \mathrm{tr}\ A dt}\) for the Wronskian determinant of the linear system \(\dot{\mathbf{x}} = A(t)\mathbf{x}\).
Published:
Problem. Show that in an hamiltonian system it is impossible to have asymptotically stable equilibrium positions and asymptotically stable limit cycles in the phase space.1
Arnol’d, V. I. (2013). Mathematical methods of classical mechanics (Vol. 60). Springer Science & Business Media. ↩
Published:

Published:
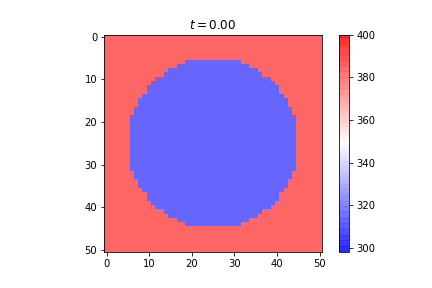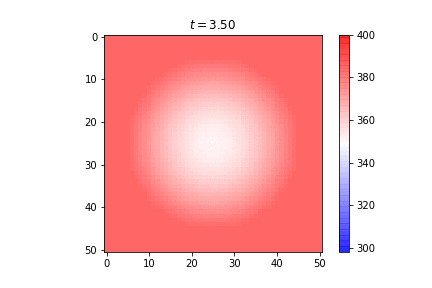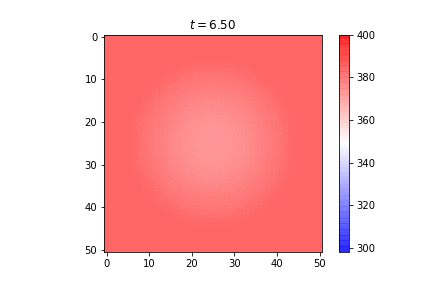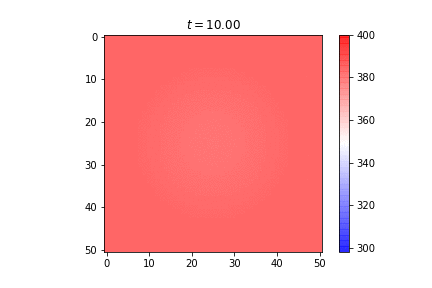
Published:
 Please refer to haoran0115/julia-set-cuda.
Please refer to haoran0115/julia-set-cuda.
Published:
Source: parallel-tempering
Published:

Published:
Under the NVT ensemble, the probability density of a particular state is given by the famous Boltzmann distribution. Note that \(Q(N,V,T)\) is the partition function, $\mathbf{x}$ denotes the phase space coordinate, $\beta=1/kT$, and $\mathcal{H}(\mathbf{x})$ is the Hamiltonian of the system.
Published:
Problem. Show that in an hamiltonian system it is impossible to have asymptotically stable equilibrium positions and asymptotically stable limit cycles in the phase space.1
Arnol’d, V. I. (2013). Mathematical methods of classical mechanics (Vol. 60). Springer Science & Business Media. ↩
Published:

Published:

Published:
Under the NVT ensemble, the probability density of a particular state is given by the famous Boltzmann distribution. Note that \(Q(N,V,T)\) is the partition function, $\mathbf{x}$ denotes the phase space coordinate, $\beta=1/kT$, and $\mathcal{H}(\mathbf{x})$ is the Hamiltonian of the system.
Published:
Source: parallel-tempering